\section{\(\underline{E X E R C I S E-I}\)}

Q.1 Determine the nature of the quadrilateral formed by four lines \(3 x+4 y-5=0 ; 4 x-3 y-5=0\); \(3 x+4 y+5=0\) and \(4 x-3 y+5=0\). Find the equation of the circle inscribed and circumscribing this quadrilateral.

Q.2 A circle \(S=0\) is drawn with its centre at \((-1,1)\) so as to touch the circle \(x^{2}+y^{2}-4 x+6 y-3=0\) externally. Find the intercept made by the circle \(\mathrm{S}=0\) on the coordinate axes.

Q.3 The line \(l \mathrm{x}+m \mathrm{y}+n=0\) intersects the curve \(\mathrm{ax}^{2}+2 h \mathrm{hy}+\mathrm{by}^{2}=1\) at the point \(\mathrm{P}\) and \(\mathrm{Q}\). The circle on PQ as diameter passes through the origin. Prove that \(n^{2}(\mathrm{a}+\mathrm{b})=l^{2}+m^{2}\).

Q.4 One of the diameters of the circle circumscribing the rectangle \(\mathrm{ABCD}\) is \(4 y=x+7\). If \(A \& B\) are the points \((-3,4) \&(5,4)\) respectively, then find the area of the rectangle.

Q.5 Find the equation to the circle which is such that the length of the tangents to it from the points \((1,0)\), \((2,0)\) and \((3,2)\) are \(1, \sqrt{7}, \sqrt{2}\) respectively.

Q.6 Let \(\mathrm{L}_{1}\) be a straight line through the origin and \(\mathrm{L}_{2}\) be the straight line \(\mathrm{x}+\mathrm{y}=1\). If the intercepts made by the circle \(\mathrm{x}^{2}+\mathrm{y}^{2}-\mathrm{x}+3 \mathrm{y}=0\) on \(\mathrm{L}_{1} \& \mathrm{~L}_{2}\) are equal, then find the equation(s) which represent \(\mathrm{L}_{1}\).

Q.7 A circle passes through the points \((-1,1),(0,6)\) and \((5,5)\). Find the points on the circle the tangents at which are parallel to the straight line joining origin to the centre.

Q.8 Find the equations of straight lines which pass through the intersection of the lines \(x-2 y-5=0\), \(7 x+y=50\) \& divide the circumference of the circle \(x^{2}+y^{2}=100\) into two arcs whose lengths are in the ratio \(2: 1\).

Q.9 In the given figure, the circle \(\mathrm{x}^{2}+\mathrm{y}^{2}=25\) intersects the \(\mathrm{x}\)-axis at the point \(\mathrm{A}\) and \(\mathrm{B}\). The line \(\mathrm{x}=11\) intersects the \(\mathrm{x}\)-axis at the point \(C\). Point \(\mathrm{P}\) moves along the line \(\mathrm{x}=11\) above the \(\mathrm{x}\)-axis and AP intersects the circle at Q. Find

(i) The coordinates of the point \(\mathrm{P}\) if the triangle \(\mathrm{AQB}\) has the maximum area.

(ii) The coordinates of the point \(\mathrm{P}\) if \(\mathrm{Q}\) is the middle point of \(\mathrm{AP}\).

(iii) The coordinates of \(\mathrm{P}\) if the area of the triangle \(\mathrm{AQB}\) is \((1 / 4)^{\text {th }}\) of the area of the triangle APC.

Q.10 A circle is drawn with its centre on the line \(x+y=2\) to touch the line \(4 x-3 y+4=0\) and pass through the point \((0,1)\). Find its equation.

Q.11 A point moving around circle \((\mathrm{x}+4)^{2}+(\mathrm{y}+2)^{2}=25\) with centre \(\mathrm{C}\) broke away from it either at the point A or point \(B\) on the circle and moved along a tangent to the circle passing through the point \(\mathrm{D}(3,-3)\). Find the following.

(i) Equation of the tangents at \(\mathrm{A}\) and \(\mathrm{B}\).

(ii) Coordinates of the points \(\mathrm{A}\) and \(\mathrm{B}\).

(iii) Angle \(\mathrm{ADB}\) and the maximum and minimum distances of the point \(\mathrm{D}\) from the circle.

(iv) Area of quadrilateral \(\mathrm{ADBC}\) and the \(\triangle \mathrm{DAB}\).

(v) Equation of the circle circumscribing the \(\triangle \mathrm{DAB}\) and also the intercepts made by this circle on the coordinate axes.

Q.12 Find the locus of the mid point of the chord of a circle \(x^{2}+y^{2}=4\) such that the segment intercepted by the chord on the curve \(x^{2}-2 x-2 y=0\) subtends a right angle at the origin.

Q.13 Find the equation of a line with gradient 1 such that the two circles \(\mathrm{x}^{2}+\mathrm{y}^{2}=4\) and \(x^{2}+y^{2}-10 x-14 y+65=0\) intercept equal length on it.

Q.14 Find the locus of the middle points of portions of the tangents to the circle \(x^{2}+y^{2}=a^{2}\) terminated by the coordinate axes. Q.15 Tangents are drawn to the concentric circles \(x^{2}+y^{2}=a^{2}\) and \(x^{2}+y^{2}=b^{2}\) at right angle to one another. Show that the locus of their point of intersection is a \(3^{\text {rd }}\) concentric circle. Find its radius.

Q.16 Find the equation of the circle passing through the three points \((4,7),(5,6)\) and \((1,8)\). Also find the coordinates of the point of intersection of the tangents to the circle at the points where it is cut by the straight line \(5 x+y+17=0\).

Q.17 Consider a circle \(\mathrm{S}\) with centre at the origin and radius 4. Four circles A, B, C and \(\mathrm{D}\) each with radius unity and centres \((-3,0),(-1,0),(1,0)\) and \((3,0)\) respectively are drawn. A chord PQ of the circle \(S\) touches the circle \(\mathrm{B}\) and passes through the centre of the circle C. If the length of this chord can be expressed as \(\sqrt{\mathrm{x}}\), find \(\mathrm{x}\).

Q.18 Obtain the equations of the straight lines passing through the point \(\mathrm{A}(2,0) \&\) making \(45^{\circ}\) angle with the tangent at A to the circle \((x+2)^{2}+(y-3)^{2}=25\). Find the equations of the circles each of radius 3 whose centres are on these straight lines at a distance of \(5 \sqrt{2}\) from \(A\).

Q.19 The line \(2 x-3 y+1=0\) is tangent to a circle \(S=0\) at \((1,1)\). If the radius of the circle is \(\sqrt{13}\). Find the equation of the circle \(\mathrm{S}\).

Q.20 Find the equation of the circle which passes through the point \((1,1) \&\) which touches the circle \(x^{2}+y^{2}+4 x-6 y-3=0\) at the point \((2,3)\) on it.

Q.21 Let \(\mathbf{K}\) denotes the square of the diameter of the circle whose diameter is the common chord of the two circles \(x^{2}+y^{2}+2 x+3 y+1=0\) and \(x^{2}+y^{2}+4 x+3 y+2=0\)

and \(\quad W\) denotes the sum of the abscissa and ordinates of a point \(P\) where all variable chords of the curve \(y^{2}=8 x\) subtending right angles at the origin, are concurrent.

and \(\quad \mathbf{H}\) denotes the square of the length of the tangent from the point \((3,0)\) on the circle \(2 x^{2}+2 y^{2}+5 y-16=0\)

Find the value of \(\mathrm{KWH}\).

Q.22 Show that the equation of a straight line meeting the circle \(\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}\) in two points at equal distances 'd' from a point \(\left(x_{1}, y_{1}\right)\) on its circumference is \(x_{1}+y_{1}-a^{2}+\left(d^{2} / 2\right)=0\).

Q.23 The radical axis of the circles \(x^{2}+y^{2}+2 g x+2 f y+c=0\) and \(2 x^{2}+2 y^{2}+3 x+8 y+2 c=0\) touches the circle \(x^{2}+y^{2}+2 x-2 y+1=0\). Show that either \(g=3 / 4\) or \(f=2\).

Q.24 Find the equation of the circle through the points of intersection of circles \(x^{2}+y^{2}-4 x-6 y-12=0\) and \(x^{2}+y^{2}+6 x+4 y-12=0 \&\) cutting the circle \(x^{2}+y^{2}-2 x-4=0\) orthogonally.

Q.25 The centre of the circle \(S=0\) lie on the line \(2 x-2 y+9=0 \& S=0\) cuts orthogonally the circle \(x^{2}+y^{2}=4\). Show that circle \(\mathrm{S}=0\) passes through two fixed points \& find their coordinates.

Q.26(a) Find the equation of a circle passing through the origin if the line pair, \(x y-3 x+2 y-6=0\) is orthogonal to it. If this circle is orthogonal to the circle \(x^{2}+y^{2}-k x+2 k y-8=0\) then find the value of \(k\).

(b) Find the equation of the circle which cuts the circle \(x^{2}+y^{2}-14 x-8 y+64=0\) and the coordinate axes orthogonally.

Q.27 Find the equation of the circle whose radius is 3 and which touches the circle \(x^{2}+y^{2}-4 x-6 y-12=0\) internally at the point \((-1,-1)\).

Q.28 Show that the locus of the centres of a circle which cuts two given circles orthogonally is a straight line \(\&\) hence deduce the locus of the centers of the circles which cut the circles \(x^{2}+y^{2}+4 x-6 y+9=0 \&\) \(x^{2}+y^{2}-5 x+4 y+2=0\) orthogonally. Interpret the locus. 

\section{EXERCISE-II}

Q.1 Find the equation of a circle which touches the line \(x+y=5\) at the point \((-2,7)\) and cuts the circle \(x^{2}+y^{2}+4 x-6 y+9=0\) orthogonally.

Q.2 Given that a right angled trapezium has an inscribed circle. Prove that the length of the right angled leg is the Harmonic mean of the lengths of bases.

Q.3 A variable circle passes through the point A(a, b) \& touches the \(\mathrm{x}\)-axis; show that the locus of the other end of the diameter through \(A\) is \((x-a)^{2}=4 b y\).

Q.4 Find the equation of the circle passing through the point \((-6,0)\) if the power of the point \((1,1)\) w.r.t. the circle is 5 and it cuts the circle \(x^{2}+y^{2}-4 x-6 y-3=0\) orthogonally.

Q.5 Consider a family of circles passing through two fixed points \(\mathrm{A}(3,7) \& \mathrm{~B}(6,5)\). The the chords in which the circle \(x^{2}+y^{2}-4 x-6 y-3=0\) cuts the members of the family are concurrent at a point. Find the coordinates of this point.

Q.6 Find the equation of circle passing through \((1,1)\) belonging to the system of co-axal circles that are tangent at \((2,2)\) to the locus of the point of intersection of mutually perpendicular tangent to the circle \(x^{2}+y^{2}=4\)

Q.7 Find the locus of the mid point of all chords of the circle \(x^{2}+y^{2}-2 x-2 y=0\) such that the pair of lines joining \((0,0) \&\) the point of intersection of the chords with the circles make equal angle with axis of \(\mathrm{x}\).

Q.8 The circle \(\mathrm{C}: \mathrm{x}^{2}+\mathrm{y}^{2}+\mathrm{kx}+(1+\mathrm{k}) \mathrm{y}-(\mathrm{k}+1)=0\) passes through the same two points for every real number k. Find

(i) the coordinates of these two points.

(ii) the minimum value of the radius of a circle \(\mathrm{C}\).

Q.9 Find the equation of a circle which is co-axial with circles \(2 x^{2}+2 y^{2}-2 x+6 y-3=0 \&\) \(x^{2}+y^{2}+4 x+2 y+1=0\). It is given that the centre of the circle to be determined lies on the radical axis of these two circles.

Q.10 The circles, which cut the family of circles passing through the fixed points \(A \equiv(2,1)\) and \(\mathrm{B} \equiv(4,3)\) orthogonally, pass through two fixed points \(\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)\) and \(\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right)\), which may be real or imaginary. Find the value of \(\left(\mathrm{x}_{1}^{3}+\mathrm{x}_{2}^{3}+\mathrm{y}_{1}^{3}+\mathrm{y}_{2}^{3}\right)\).

Q.11 A circle with center in the first quadrant is tangent to \(y=x+10, y=x-6\), and the \(y\)-axis. Let \((h, k)\) be the center of the circle. If the value of \((h+k)=a+b \sqrt{a}\) where \(\sqrt{a}\) is a surd, find the value of \(a+b\).

Q.12 A circle \(\mathrm{C}\) is tangent to the \(\mathrm{x}\) and \(\mathrm{y}\) axis in the first quadrant at the points \(\mathrm{P}\) and \(\mathrm{Q}\) respectively. \(\mathrm{BC}\) and \(\mathrm{AD}\) are parallel tangents to the circle with slope - 1. If the points \(\mathrm{A}\) and \(\mathrm{B}\) are on the \(\mathrm{y}\)-axis while \(\mathrm{C}\) and D are on the \(\mathrm{x}\)-axis and the area of the figure \(\mathrm{ABCD}\) is \(900 \sqrt{2}\) sq. units then find the radius of the circle.

Q.13 Let A, B, C be real numbers such that

(i) \((\sin \mathrm{A}, \cos \mathrm{B})\) lies on a unit circle centred at origin.

(ii) \(\tan \mathrm{C}\) and \(\cot \mathrm{C}\) are defined.

If the minimum value of \((\tan C-\sin A)^{2}+(\cot C-\cos B)^{2}\) is \(a+b \sqrt{2}\) where \(a, b \in I\), find the value of \(a^{3}+b^{3}\).

Q.14 An isosceles right angled triangle whose sides are 1,1, \(\sqrt{2}\) lies entirely in the first quadrant with the ends of the hypotenuse on the coordinate axes. If it slides prove that the locus of its centroid is \((3 x-y)^{2}+(x-3 y)^{2}=\frac{32}{9}\). Q.15 A rhombus \(\mathrm{ABCD}\) has sides of length 10. A circle with centre 'A' passes through \(\mathrm{C}\) (the opposite vertex) likewise, a circle with centre B passes through \(D\). If the two circles are tangent to each other, find the area of the rhombus.

Q.16 Find the equation of a circle which touches the lines \(7 x^{2}-18 x y+7 y^{2}=0\) and the circle \(x^{2}+y^{2}-8 x-8 y=0\) and is contained in the given circle.

Q.17 Find the equation of the circle which passes through the origin, meets the \(\mathrm{x}\)-axis orthogonally \& cuts the circle \(x^{2}+y^{2}=a^{2}\) at an angle of \(45^{\circ}\).

Q.18 Circles \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) are externally tangent and they are both internally tangent to the circle \(\mathrm{C}_{3}\). The radii of \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) are 4 and 10, respectively and the centres of the three circles are collinear. \(\mathrm{A}^{\text {chord of }} \mathrm{C}_{3}\) is also a common internal tangent of \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\). Given that the length of the chord is \(\frac{\mathrm{m} \sqrt{\mathrm{n}}}{\mathrm{p}}\) where \(m, n\) and \(p\) are positive integers, \(m\) and \(p\) are relatively prime and \(n\) is not divisible by the square of any prime, find the value of \((m+n+p)\).

\section{EXERCISE-III}

Q.1 (a) The triangle \(P Q R\) is inscribed in the circle, \(x^{2}+y^{2}=25\). If \(Q\) and \(R\) have co-ordinates \((3,4) \&\) \((-4,3)\) respectively, then \(\angle\) QPR is equal to :

(A) \(\frac{\pi}{2}\)

(B) \(\frac{\pi}{3}\)

(C) \(\frac{\pi}{4}\)

(D) \(\frac{\pi}{6}\)

(b) If the circles, \(x^{2}+y^{2}+2 x+2 k y+6=0 \& x^{2}+y^{2}+2 k y+k=0\) intersect orthogonally, then ' \(k\) ' is :

(A) 2 or \(-\frac{3}{2}\)

(B) \(-2\) or \(-\frac{3}{2}\)

(C) 2 or \(\frac{3}{2}\)

(D) \(-2\) or \(\frac{3}{2}\)

[ JEE '2000 (Screening) \(1+1\) ]

Q.2 (a) Extremities of a diagonal of a rectangle are \((0,0) \&(4,3)\). Find the equation of the tangents to the circumcircle of a rectangle which are parallel to this diagonal.

(b) Find the point on the straight line, \(y=2 x+11\) which is nearest to the circle, \(16\left(x^{2}+y^{2}\right)+32 x-8 y-50=0\).

(c) A circle of radius 2 units rolls on the outerside of the circle, \(x^{2}+y^{2}+4 x=0\), touching it externally. Find the locus of the centre of this outer circle. Also find the equations of the common tangents of the two circles when the line joining the centres of the two circles is inclined at an angle of \(60^{\circ}\) with \(\mathrm{x}\)-axis.

[REE '2000 (Mains) \(3+3+5]\)

Q.3 (a) Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius \(r\). If PS and \(R Q\) intersect at a point \(X\) on the circumference of the circle then \(2 \mathrm{r}\) equals

(A) \(\sqrt{\mathrm{PQ} \cdot \mathrm{RS}}\)

(B) \(\frac{P Q+R S}{2}\)

(C) \(\frac{2 \mathrm{PQ} \cdot \mathrm{RS}}{\mathrm{PQ}+\mathrm{RS}}\)

(D) \(\sqrt{\frac{(\mathrm{PQ})^{2}+(\mathrm{RS})^{2}}{2}}\)

[ JEE '2001 (Screening) 1 out of 35]

(b) Let \(2 x^{2}+y^{2}-3 x y=0\) be the equation of a pair of tangents drawn from the origin 'O' to a circle of radius 3 with centre in the first quadrant. If \(A\) is one of the points of contact, find the length of \(\mathrm{OA}\).

[JEE '2001 (Mains) 5 out of 100]

Q.4 (a) Find the equation of the circle which passes through the points of intersection of circles \(x^{2}+y^{2}-2 x-6 y+6=0\) and \(x^{2}+y^{2}+2 x-6 y+6=0\) and intersects the circle \(x^{2}+y^{2}+4 x+6 y+4=0\) orthogonally.

[ REE '2001 (Mains) 3 out of 100 ]

(b) Tangents TP and TQ are drawn from a point \(T\) to the circle \(x^{2}+y^{2}=a^{2}\). If the point \(T\) lies on the line \(p x+q y=r\), find the locus of centre of the circumcircle of triangle TPQ.

[ REE '2001 (Mains) 5 out of 100 ] Q.5 (a) If the tangent at the point \(P\) on the circle \(x^{2}+y^{2}+6 x+6 y=2\) meets the straight line \(5 x-2 y+6=0\) at a point \(Q\) on the \(y\)-axis, then the length of PQ is

(A) 4

(B) \(2 \sqrt{5}\)

(C) 5

(D) \(3 \sqrt{5}\)

(b) If \(a>2 b>0\) then the positive value of \(m\) for which \(y=m x-b \sqrt{1+m^{2}}\) is a common tangent to \(x^{2}+y^{2}=b^{2}\) and \((x-a)^{2}+y^{2}=b^{2}\) is

(A) \(\frac{2 b}{\sqrt{a^{2}-4 b^{2}}}\)

(B) \(\frac{\sqrt{a^{2}-4 b^{2}}}{2 b}\)

(C) \(\frac{2 b}{a-2 b}\)

(D) \(\frac{b}{a-2 b}\)

[ JEE '2002 (Scr)3 + 3 out of 270]

Q.6 The radius of the circle, having centre at \((2,1)\), whose one of the chord is a diameter of the circle \(\mathrm{x}^{2}+\mathrm{y}^{2}-2 \mathrm{x}-6 \mathrm{y}+6=0\)

(A) 1

(B) 2

(C) 3

(D) \(\sqrt{3} \quad\) [JEE '2004 (Scr)]

Q.7 Line \(2 x+3 y+1=0\) is a tangent to a circle at \((1,-1)\). This circle is orthogonal to a circle which is drawn having diameter as a line segment with end points \((0,-1)\) and \((-2,3)\). Find equation of circle.

[JEE '2004, 4 out of 60]

Q.8 A circle is given by \(\mathrm{x}^{2}+(y-1)^{2}=1\), another circle \(\mathrm{C}\) touches it externally and also the \(\mathrm{x}\)-axis, then the locus of its centre is

(A) \(\left\{(x, y): x^{2}=4 y\right\} \cup\{(x, y): y \leq 0\}\)

(C) \(\left\{(x, y): x^{2}=y\right\} \cup\{(0, y): y \leq 0\}\)

(B) \(\left.\left\{(\mathrm{x}, \mathrm{y}): \mathrm{x}^{2}+(\mathrm{y}-1)^{2}=4\right\} \cup\{\mathrm{x}, \mathrm{y}): \mathrm{y} \leq 0\right\}\)

(D) \(\left\{(x, y): x^{2}=4 y\right\} \cup\{(0, y): y \leq 0\}\)

[JEE '2005 (Scr)]

Q.9(a) Let \(\mathrm{ABCD}\) be a quadrilateral with area 18 , with side \(\mathrm{AB}\) parallel to the side \(\mathrm{CD}\) and \(\mathrm{AB}=2 \mathrm{CD}\). Let \(\mathrm{AD}\) be perpendicular to \(\mathrm{AB}\) and \(\mathrm{CD}\). If a circle is drawn inside the quadrilateral \(\mathrm{ABCD}\) touching all the sides, then its radius is

(A) 3

(B) 2

(C) \(3 / 2\)

(D) 1

(b) Tangents are drawn from the point \((17,7)\) to the circle \(x^{2}+y^{2}=169\).

Statement-1: The tangents are mutually perpendicular.

because

Statement-2: The locus of the points from which mutually perpendicular tangents can be drawn to the given circle is \(x^{2}+y^{2}=338\).

(A) Statement-1 is true, statement-2 is true; statement- 2 is correct explanation for statement-1.

(B) Statement-1 is true, statement-2 is true; statement-2 is NOT a correct explanation for statement-1.

(C) Statement-1 is true, statement- 2 is false.

(D) Statement- 1 is false, statement- 2 is true.

[JEE 2007, 3+3]

Q.10(a) Consider the two curves

\[

C_{1}: y^{2}=4 x \quad ; \quad C_{2}: x^{2}+y^{2}-6 x+1=0 \text {. Then, }

\]

(A) \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) touch each other only at one point

(B) \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) touch each other exactly at two points

(C) \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) intersect (but do not touch) at exactly two points

(D) \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) neither intersect nor touch each other

(b) Consider, \(\quad \mathrm{L}_{1}: 2 \mathrm{x}+3 \mathrm{y}+\mathrm{P}-3=0 \quad ; \quad \mathrm{L}_{2}: 2 \mathrm{x}+3 \mathrm{y}+\mathrm{P}+3=0\), where \(p\) is a real number, and \(C: x^{2}+y^{2}+6 x-10 y+30=0\).

STATEMENT-1 : If line \(\mathrm{L}_{1}\) is a diameter of circle \(\mathrm{C}\), then line \(\mathrm{L}_{2}\) is not always a diameter of circle \(\mathrm{C}\). and

STATEMENT-2 : If line \(\mathrm{L}_{1}\) is a diameter of circle \(\mathrm{C}\), then line \(\mathrm{L}_{2}\) is not a chord of circle \(\mathrm{C}\).

(A) Statement-1 is True, Statement-2 is True; statement-2 is a correct explanation for statement-1

(B) Statement-1 is True, Statement-2 is True; statement- 2 is NOT a correct explanation for statement-1

(C) Statement-1 is True, Statement-2 is False

(D) Statement-1 is False, Statement-2 is True (c) Comprehension ( 3 questions together):

A circle \(C\) of radius 1 is inscribed in an equilateral triangle \(P Q R\). The points of contact of \(\mathrm{C}\) with the sides \(P Q, Q R, R P\) are \(D, E, F\) respectively. The line \(P Q\) is given by the equation \(\sqrt{3} x+y-6=0\) and the point \(\mathrm{D}\) is \(\left(\frac{3 \sqrt{3}}{2}, \frac{3}{2}\right)\). Further, it is given that the origin and the centre of \(\mathrm{C}\) are on the same side of the line PQ.

(i) The equation of circle \(\mathrm{C}\) is

(A) \((x-2 \sqrt{3})^{2}+(y-1)^{2}=1\)

(B) \((x-2 \sqrt{3})^{2}+\left(y+\frac{1}{2}\right)^{2}=1\)

(C) \((x-\sqrt{3})^{2}+(y+1)^{2}=1\)

(D) \((x-\sqrt{3})^{2}+(y-1)^{2}=1\)

(ii) Points \(\mathrm{E}\) and \(\mathrm{F}\) are given by

(A) \(\left(\frac{\sqrt{3}}{2}, \frac{3}{2}\right),(\sqrt{3}, 0)\)

(B) \(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right),(\sqrt{3}, 0)\)

(C) \(\left(\frac{\sqrt{3}}{2}, \frac{3}{2}\right),\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\)

(D) \(\left(\frac{3}{2}, \frac{\sqrt{3}}{2}\right),\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\)

(iii) Equations of the sides \(\mathrm{RP}, \mathrm{RQ}\) are

(A) \(y=\frac{2}{\sqrt{3}} x+1, y=-\frac{2}{\sqrt{3}} x-1\)

(B) \(y=\frac{1}{\sqrt{3}} x, y=0\)

(C) \(y=\frac{\sqrt{3}}{2} x+1, y=-\frac{\sqrt{3}}{2} x-1\)

(D) \(y=\sqrt{3} x, y=0\)

\([\mathrm{JEE} 2008,3+3+4+4+4]\)

Q.11(a) Tangents drawn from the point \(\mathrm{P}(1,8)\) to the circle

\[

x^{2}+y^{2}-6 x-4 y-11=0

\]

touch the circle at the points \(A\) and \(B\). The equation of the circumcircle of the triangle \(\mathrm{PAB}\) is

(A) \(x^{2}+y^{2}+4 x-6 y+19=0\)

(C) \(x^{2}+y^{2}-2 x+6 y-29=0\)

(B) \(x^{2}+y^{2}-4 x-10 y+19=0\)

(D) \(x^{2}+y^{2}-6 x-4 y+19=0\)

(b) The centres of two circles \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) each of unit radius are at a distance of 6 units from each other. Let \(\mathrm{P}\) be the mid point of the line segment joining the centres of \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) and \(\mathrm{C}\) be a circle touching circles \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) externally. If a common tangent to \(\mathrm{C}_{1}\) and \(\mathrm{C}\) passing through \(\mathrm{P}\) is also a common tangent to \(\mathrm{C}_{2}\) and \(\mathrm{C}\), then the radius of the circle \(\mathrm{C}\) is

\([\mathrm{JEE} 2009,3+4]\) Q.1 square of side \(2 ; x^{2}+y^{2}=1 ; x^{2}+y^{2}=2\)

Q.2 zero, zero

Q.5 \(\left.2\left(x^{2}+y^{2}\right)+6 x-17 y-6=0\right]\)

Q.7 \((5,1) \&(-1,5)\)

Q.8 \(4 x-3 y-25=0\) OR \(3 x+4 y-25=0\)

Q.9 (i) \((11,16)\), (ii) \((11,8)\), (iii) \((11,12)\)

Q.10 \(x^{2}+y^{2}-2 x-2 y+1=0\) OR \(x^{2}+y^{2}-42 x+38 y-39=0\)

Q.11 (i) \(3 \mathrm{x}-4 \mathrm{y}=21 ; 4 \mathrm{x}+3 \mathrm{y}=3\); (ii) \(\mathrm{A}(0,1)\) and \(\mathrm{B}(-1,-6)\); (iii) \(90^{\circ}, 5(\sqrt{2} \pm 1)\) units (iv) 25 sq. units, \(12.5\) sq. units; (v) \(x^{2}+y^{2}+x+5 y-6, x\) intercept 5 ; y intercept 7

Q.12 \(x^{2}+y^{2}-2 x-2 y=0\)

Q.14 \(a^{2}\left(x^{2}+y^{2}\right)=4 x^{2} y^{2}\)

Q.16 \((-4,2), x^{2}+y^{2}-2 x-6 y-15=0\)

Q.18 \(x-7 y=2,7 x+y=14 ;(x-1)^{2}+(y-7)^{2}=3^{2} ;(x-3)^{2}+(y+7)^{2}=3^{2}\); \((x-9)^{2}+(y-1)^{2}=3^{2} ;(x+5)^{2}+(y+1)^{2}=3^{2}\)

Q.19 \(x^{2}+y^{2}-6 x+4 y=0\) OR \(x^{2}+y^{2}+2 x-8 y+4=0\)

Q.20 \(x^{2}+y^{2}+x-6 y+3=0\)

Q.24 \(x^{2}+y^{2}+16 x+14 y-12=0\)

Q.26 (a) \(x^{2}+y^{2}+4 x-6 y=0 ; k=1 ;\) (b) \(x^{2}+y^{2}=64\)

Q.27 \(5 x^{2}+5 y^{2}-8 x-14 y-32=0\) Q.21 64

Q.25 \((-4,4) ;(-1 / 2,1 / 2)\)

Q.13 \(2 x-2 y-3=0\)

Q.15 \(x^{2}+y^{2}=a^{2}+b^{2} ; r=\sqrt{a^{2}+b^{2}}\)

Q.28 \(9 x-10 y+7=0\); radical axis

\section{\(\underline{E X E R C I S E-I I}\)}

Q.1 \(\quad x^{2}+y^{2}+7 x-11 y+38=0 \quad\) Q.4 \(\quad x^{2}+y^{2}+6 x-3 y=0 \quad\) Q.5 \(\quad\left(2, \frac{23}{3}\right)\)

Q.6 \(\quad x^{2}+y^{2}-3 x-3 y+4=0 \quad\) Q.7 \(\quad x+y=2 \quad\) Q.8 \(\quad(1,0) \&(1 / 2,1 / 2) ; r=\frac{1}{2 \sqrt{2}}\)

\(\begin{array}{llllllll}\text { Q.9 } & 4 x^{2}+4 y^{2}+6 x+10 y-1=0 & \text { Q.10 } & 40 & \text { Q.11 } & 10 & \text { Q.12 } & r=15\end{array}\)

\(\begin{array}{llllll}\text { Q.13 } & 19 & \text { Q.15 } & 75 \text { sq. unit } & \text { Q.16 } & x^{2}+y^{2}-12 x-12 y+64=0\end{array}\)

Q.17 \(x^{2}+y^{2} \pm a \sqrt{2} x=0 \quad\) Q.18 19

\section{EXERCISE-III}

Q.1 (a) \(\mathrm{C}\) (b) \(\mathrm{A}\)

Q.2 (a) \(6 x-8 y+25=0 \quad \& \quad 6 x-8 y-25=0 ; \quad\) (b) \((-9 / 2,2)\)

(c) \(x^{2}+y^{2}+4 x-12=0, T_{1}: \sqrt{3} x-y+2 \sqrt{3}+4=0, T_{2}: \sqrt{3} x-y+2 \sqrt{3}-4=0\) (D.C.T.)

\[

\mathrm{T}_{3}: \mathrm{x}+\sqrt{3} \mathrm{y}-2=0, \mathrm{~T}_{4}: \mathrm{x}+\sqrt{3} \mathrm{y}+6=0 \text { (T.C.T.) }

\]

Q.3 (a) \(\mathrm{A} ; \quad\) (b) \(\mathrm{OA}=3(3+\sqrt{10})\)

Q.5 (a) \(\mathrm{C}\); (b) \(\mathrm{A}\)

Q.7 \(2 x^{2}+2 y^{2}-10 x-5 y+1=0\)

Q.10 (a) B; (b) \(\mathrm{C}\); (c) (i) \(\mathrm{D}\), (ii) \(\mathrm{A}\), (iii) \(\mathrm{D}\) Q.4 (a) \(x^{2}+y^{2}+14 x-6 y+6=0\);

(b) \(2 p x+2 q y=r\)

\section{Q.6 C}

Q.8 D

Q.9 (a) B; (b) \(\mathrm{A}\)

Q.11 (a) B; (b) 8 

\section{New for 11th PQRS 2009}

Q.6 Let \(\mathrm{L}_{1}\) be a straight line through the origin and \(\mathrm{L}_{2}\) be the straight line \(\mathrm{x}+\mathrm{y}=1\). If the intercepts made by the circle \(\mathrm{x}^{2}+\mathrm{y}^{2}-\mathrm{x}+3 \mathrm{y}=0\) on \(\mathrm{L}_{1}\) and \(\mathrm{L}_{2}\) are equal, then find the equations which represent \(\mathrm{L}_{1}\).

[Ans. \(x-y=0 ; x+7 y=0] \quad\) [JEE '99,3 (out of 200)]

\section{New for 11th PQRS 2009}

\section{EXERCISE-II CIRCLE}

Q.1 Find the equation of a circle which touches the line \(x+y=5\) at the point \((-2,7)\) and cuts the circle \(x^{2}+y^{2}+4 x-6 y+9=0\) orthogonally.

[Ans. \(\left.x^{2}+y^{2}+7 x-11 y+38=0\right] \quad[\) REE '98,6 \(]\)

\section{New for 11th PQRS 2009}

Q.2 Given that a right angled trapezium has an inscribed circle. Prove that the length of the right angled leg is the Harmonic mean of the lengths of bases.

[Sol. length of the right angled leg \(=\mathrm{AO} \quad\) [12th, 23-08-2009, P-1] equation of circle is, [T/S, Q.2, Ex-2, Circle] done

\[

(x-r)^{2}+(y-r)^{2}=r^{2}

\]

put \(x=x_{1}, y=2 r\) to get square of the tangent from \(B\)

\(\mathrm{L}^{2}=\left(\mathrm{x}_{1}-\mathrm{r}\right)^{2}+\mathrm{r}^{2}-\mathrm{r}^{2}\)

\(\mathrm{L}=\mathrm{x}_{1}-\mathrm{r}=\mathrm{BP}=\mathrm{BQ}\)

\(\|\) lly \(\quad \mathrm{x}_{2}-\mathrm{r}=\mathrm{PC} \quad\left(\right.\) Hence \(\left.\mathrm{BC}=\mathrm{BP}+\mathrm{PC}=\mathrm{x}_{1}+\mathrm{x}_{2}-2 \mathrm{r}\right)\)


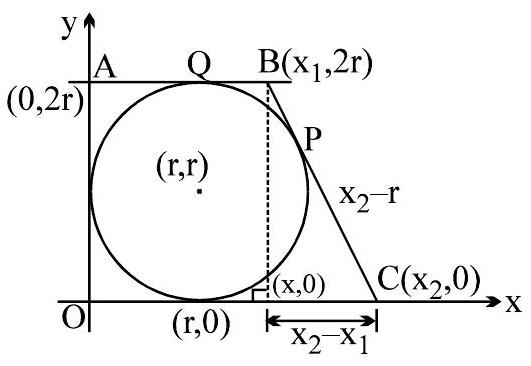
hence \(\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+4 \mathrm{r}^{2}=\left(\mathrm{x}_{1}+\mathrm{x}_{2}-2 \mathrm{r}\right)^{2}\)

\(\left(x_{2}+x_{1}\right)^{2}-4 x_{1} x_{2}+4 r^{2}=\left(x_{2}+x_{1}\right)^{2}+4 r^{2}-4 r\left(x_{1}+x_{2}\right)\)

\(\mathrm{x}_{1} \mathrm{x}_{2}=\mathrm{r}\left(\mathrm{x}_{1}+\mathrm{x}_{2}\right)\)

\(\frac{1}{\mathrm{r}}=\frac{1}{\mathrm{x}_{1}}+\frac{1}{\mathrm{x}_{2}} \Rightarrow 2 \mathrm{r}=\frac{2 \mathrm{x}_{1} \mathrm{x}_{2}}{\mathrm{x}_{1}+\mathrm{x}_{2}} \Rightarrow \quad\) OA is H.M. of the lengths of bases Ans.]

\section{EXERCISE-II CIRCLE}

Q.8 The circles, which cut the family of circles passing through the fixed points \(A \equiv(2,1)\) and \(\mathrm{B} \equiv(4,3)\) orthogonally, pass through two fixed points \(\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)\) and \(\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right)\), which may be real or imaginary. Find the value of \(\left(x_{1}^{3}+x_{2}^{3}+y_{1}^{3}+y_{2}^{3}\right)\).

[Ans. 40]

[Sol. The equation of circle taking \(\mathrm{AB}\) as diameter \(\quad\) [12th, 24-08-2008]

\[

(x-2)(x-4)+(y-1)(y-3)=0

\]

The equation of the line joining the points \(\mathrm{A}\) and \(\mathrm{B}\) is

\[

\mathrm{x}-\mathrm{y}-1=0 \quad \text {....(2) }

\]

The equation of members of family of circle passing through \(A\) and \(\mathrm{B}\) is given by

\[

\begin{array}{lll} 

& \mathrm{S} \equiv(\mathrm{x}-2)(\mathrm{x}-4)+(\mathrm{y}-1)(\mathrm{y}-3)+\lambda(\mathrm{x}-\mathrm{y}-1)=0 & \text { where } \lambda \text { is parameter, } \lambda \in \mathrm{R} \\

\therefore \quad \mathrm{S} \equiv \mathrm{x}^{2}+\mathrm{y}^{2}+(\lambda-6) \mathrm{x}+(-\lambda-4) \mathrm{y}+(11-\lambda)=0 & \ldots . .(1)

\end{array}

\]

Let the circles which cuts the members of circle be

\[

S_{1}=x^{2}+y^{2}+2 g x+2 f y+c=0

\]

Applying condition of orthogonality for (1) and (2), we get

\[

x^{2}+y^{2}+2\left(\frac{-c-15}{10}\right) x+2\left(\frac{-c-5}{10}\right) y+c=0

\]

or \(\quad x^{2}+y^{2}-3 x-y-\frac{c}{5}(x+y-5)=0\) \(2 \mathrm{~g}\left(\frac{\lambda-6}{2}\right)+2 \mathrm{f}\left(\frac{-\lambda-4}{2}\right)=\mathrm{c}+11-\lambda\)

i.e. \(\quad(-6 g-4 f-c-11)+\lambda(g-f+1)=0\)

This will also hold for all \(\lambda \in \mathrm{R}\)

\(\therefore \quad\) we have \(\quad-6 \mathrm{~g}-4 \mathrm{f}-\mathrm{c}-11=0\) and \(\mathrm{g}-\mathrm{f}+1=0\)

solving these equations for \(g\) and \(f\) in terms of \(c\), we get \(g=\frac{-c-15}{10}\) and \(f=\frac{-c-5}{10}\)

substituting the values of \(g\) and \(f\) in terms of \(c\) in (2), we get the circles cutting the circles of system (1) orthogonally as

which represents equation of family of circles passing through two fixed points whose coordinates obtained by solving equations

i.e. solving \(x^{2}+y^{2}-3 x-y=0\) and \(x+y-5=0\)

\(\Rightarrow \quad \mathrm{x}^{2}-6 \mathrm{x}-10=0(\mathrm{D}<0)\)

Illy \(\quad y^{2}-4 y+5=0\)

\(y_{1}+y_{2}=4 ; \quad y_{1} y_{2}=5\)

\(\left(x_{1}^{3}+x_{2}^{3}+y_{1}^{3}+y_{2}^{3}\right)=\left(x_{1}+x_{2}\right)^{3}-3 x_{1} x_{2}\left(x_{1}+x_{2}\right)+\left(y_{1}+y_{2}\right)^{3}-3 y_{1} y_{2}\left(y_{1}+y_{2}\right)\)

\(=216-30(6)+64-60\)

\(=36+4=40\) Ans. \(]\)

\section{EXERCISE-III CIRCLE}

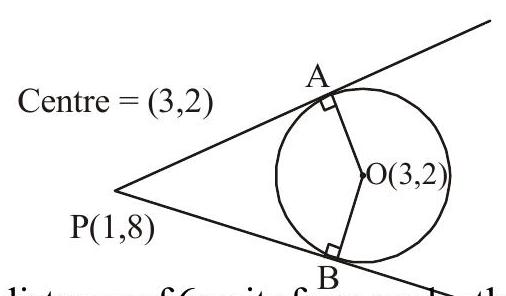
@Q.11(a) Tangents drawn from the point \(\mathrm{P}(1,8)\) to the circle

\[

x^{2}+y^{2}-6 x-4 y-11=0

\]

touch the circle at the points A and \(B\). The equation of the circumcircle of the triangle \(\mathrm{PAB}\) is

(A) \(x^{2}+y^{2}+4 x-6 y+19=0\)

(C) \(x^{2}+y^{2}-2 x+6 y-29=0\)

(B) \(x^{2}+y^{2}-4 x-10 y+19=0\)

(D) \(x^{2}+y^{2}-6 x-4 y+19=0\)

\([3]\)

\([\) Sol. \([\mathbf{B}]\)

Circumcircle of \(\triangle \mathrm{PAB}\) will pass through the centre of circle i.e. circle of diammetrical form

\[

\begin{aligned}

& (x-1)(x-3)+(y-8)(y-2)=0 \\

& x^{2}+y^{2}-4 x-10 y+19=0 \Rightarrow

\end{aligned}

\]


(a) The centres of two circles \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) each of unit radius are at a distance of 6 units from each other. Let \(\mathrm{P}\) be the mid point of the line segment joining the centres of \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) and \(\mathrm{C}\) be a circle touching circles \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) externally. If a common tangent to \(\mathrm{C}_{1}\) and \(\mathrm{C}\) passing through \(\mathrm{P}\) is also a common tangent to \(\mathrm{C}_{2}\) and \(\mathrm{C}\), then the radius of the circle \(\mathrm{C}\) is

[Ans. 8]

[4]

[Sol. 


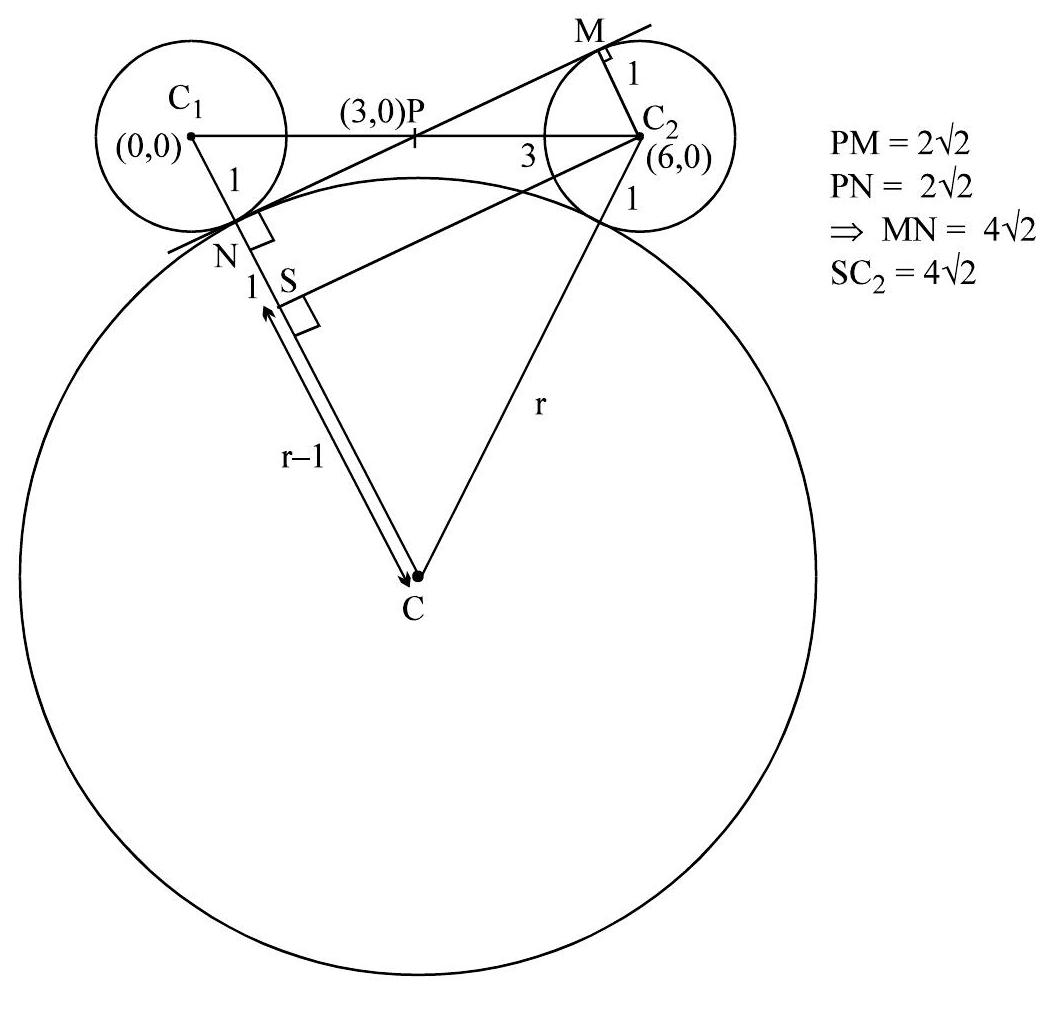
from figure

\(32+(\mathrm{r}-1)^{2}=(\mathrm{r}+1)^{2} \Rightarrow \quad 32=4 \mathrm{r} \Rightarrow \mathrm{r}=8\) Ans. ]