POSITION OFA POINT RELATIVE TO A PARABOLA:

The point \(\left(\mathrm{x}_{1} \mathrm{y}_{1}\right)\) lies outside, on or inside the parabola \(\mathrm{y}^{2}=4 \mathrm{ax}\) according as the expression \(\mathrm{y}_{1}^{2}-4 \mathrm{ax}_{1}\) is positive, zero or negative.

LINE &   A PARABOLA :

The line \(y=m x+c\) meets the parabola \(y^{2}=4 a x\) in two points real, coincident or imaginary according as \(\mathrm{a}>\mathrm{cm} \Rightarrow\) condition of tangency is, \(\mathrm{c}=\frac{\mathrm{a}}{\mathrm{m}}\).

7. Length of the chord intercepted by the parabola on the line \(y=m x+c\) is : \(\left(\frac{4}{m^{2}}\right) \sqrt{a\left(1+m^{2}\right)(a-m c)}\). Note: length of the focal chord making an angle \(\alpha\) with the \(\mathrm{x}\)-axis is \(4 \mathrm{aCosec}^{2} \alpha\).

PARAMETRIC REPRESENTATION :

The simplest & the best form of representing the co-ordinates of a point on the parabola is (at \(\left.{ }^{2}, 2 a t\right)\). The equations \(x=a t^{2} \& y=2\) at together represents the parabola \(y^{2}=4 a x, t\) being the parameter. The equation of a chord joining \(\mathrm{t}_{1} \& \mathrm{t}_{2}\) is \(2 \mathrm{x}-\left(\mathrm{t}_{1}+\mathrm{t}_{2}\right) \mathrm{y}+2 \mathrm{at}_{1} \mathrm{t}_{2}=0\).

Note: If the chord joining \(t_{1}, t_{2} \& t_{3}, t_{4}\) pass through a point \((c, 0)\) on the axis, then \(t_{1} t_{2}=t_{3} t_{4}=-c / a\).

TANGENTS TO THE PARABOLA \(\mathrm{y}^{2}=4 \mathrm{ax}\) :

(i) \(\quad \mathrm{y}_{1}=2 \mathrm{a}\left(\mathrm{x}+\mathrm{x}_{1}\right)\) at the point \(\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)\);

(ii) \(\quad y=m x+\frac{a}{m}(m \neq 0)\) at \(\left(\frac{a}{m^{2}}, \frac{2 a}{m}\right)\)

(iii) \(\mathrm{ty}=\mathrm{x}+\mathrm{at} \mathrm{t}^{2}\) at \(\left(\mathrm{at}^{2}, 2 \mathrm{at}\right)\).

Note : Point of intersection of the tangents at the point \(\mathrm{t}_{1} \& \mathrm{t}_{2}\) is \(\left[a \mathrm{t}_{1} \mathrm{t}_{2,} a\left(\mathrm{t}_{1}+\mathrm{t}_{2}\right)\right]\).

10. NORMALS TO THE PARABOLA \(y^{2}=4 a x\) :

(i) \(\mathrm{y}-\mathrm{y}_{1}=-\frac{\mathrm{y}_{1}}{2 \mathrm{a}}\left(\mathrm{x}-\mathrm{x}_{1}\right)\) at \(\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)\);

(ii) \(y=m x-2 a m-a m^{3} a t\left(a^{2}-2 a m\right)\)

(iii) \(y+t x=2 a t+a t^{3} a t\left(a t^{2}, 2 a t\right)\).

Note : Point of intersection of normals at \(\mathrm{t}_{1} \& \mathrm{t}_{2}\) are, \(\mathrm{a}\left(\mathrm{t}_{1}^{2}+\mathrm{t}_{2}^{2}+\mathrm{t}_{1} \mathrm{t}_{2}+2\right) ;-\mathrm{at}_{1} \mathrm{t}_{2}\left(\mathrm{t}_{1}+\mathrm{t}_{2}\right)\).

THREE VERY IMPORTANT RESULTS :

(a) If \(\mathrm{t}_{1} \& \mathrm{t}_{2}\) are the ends of a focal chord of the parabola \(\mathrm{y}^{2}=4 a x\) then \(\mathrm{t}_{1} \mathrm{t}_{2}=-1\). Hence the co-ordinates at the extremities of a focal chord can be taken as \(\left(a t^{2}, 2 a t\right) \&\left(\frac{a}{t^{2}},-\frac{2 a}{t}\right)\).

(b) If the normals to the parabola \(y^{2}=4 a x\) at the point \(t_{1}\), meets the parabola again at the point \(\mathrm{t}_{2}\), then \(\mathrm{t}_{2}=-\left(\mathrm{t}_{1}+\frac{2}{\mathrm{t}_{1}}\right)\)

(c) If the normals to the parabola \(y^{2}=4 a x\) at the points \(t_{1} \& t_{2}\) intersect again on the parabola at the point ' \(t_{3}\) ' then \(\mathrm{t}_{1} \mathrm{t}_{2}=2 ; \mathrm{t}_{3}=-\left(\mathrm{t}_{1}+\mathrm{t}_{2}\right)\) and the line joining \(\mathrm{t}_{1} \& \mathrm{t}_{2}\) passes through a fixed point \((-2 \mathrm{a}, 0)\).

General Note :

(i) Length of subtangent at any point \(\mathrm{P}(\mathrm{x}, \mathrm{y})\) on the parabola \(\mathrm{y}^{2}=4 \mathrm{ax}\) equals twice the abscissa of the point P. Note that the subtangent is bisected at the vertex.

(ii) Length of subnormal is constant for all points on the parabola \& is equal to the semi latus rectum.

(iii) If a family of straight lines can be represented by an equation \(\lambda^{2} \mathrm{P}+\lambda \mathrm{Q}+\mathrm{R}=0\) where \(\lambda\) is a parameter and \(P, Q, R\) are linear functions of \(x\) and \(y\) then the family of lines will be tangent to the curve \(Q^{2}=4 P R\).

12. The equation to the pair of tangents which can be drawn from any point \(\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)\) to the parabola \(\mathrm{y}^{2}=4 a x\) is given by: \(\mathrm{SS}_{1}=\mathrm{T}^{2}\) where :

\(\mathrm{S} \equiv \mathrm{y}^{2}-4 \mathrm{ax} \quad ; \quad \mathrm{S}_{1}=\mathrm{y}_{1}^{2}-4 \mathrm{ax}_{1} \quad ; \quad \mathrm{T} \equiv \mathrm{y} \mathrm{y}_{1}-2 \mathrm{a}\left(\mathrm{x}+\mathrm{x}_{1}\right)\). (d) Any tangent to a parabola \& the perpendicular on it from the focus meet on the tangtent at the vertex.

(e) If the tangents at \(\mathrm{P}\) and \(\mathrm{Q}\) meet in \(\mathrm{T}\), then:

TP and TQ subtend equal angles at the focus \(\mathrm{S}\).

\(\mathrm{ST}^{2}=\) SP. SQ &        ■ The triangles SPT and STQ are similar.

(f) Tangents and Normals at the extremities of the latus rectum of a parabola \(y^{2}=4 a x\) constitute a square, their points of intersection being \((-a, 0) \&(3,0)\).

(g) Semi latus rectum of the parabola \(y^{2}=4 a x\), is the harmonic mean between segments of any focal chord of the parabola is ; \(2 a=\frac{2 b c}{b+c}\) i.e. \(\frac{1}{b}+\frac{1}{c}=\frac{1}{a}\).

The circle circumscribing the triangle formed by any three tangents to a parabola passes through the focus.

(i) The orthocentre of any triangle formed by three tangents to a parabola \(y^{2}=4 a x\) lies on the directrix \& has the co-ordinates \(-\mathrm{a}, \mathrm{a}\left(\mathrm{t}_{1}+\mathrm{t}_{2}+\mathrm{t}_{3}+\mathrm{t}_{1} \mathrm{t}_{2} \mathrm{t}_{3}\right)\).

(j) The area of the triangle formed by three points on a parabola is twice the area of the triangle formed by the tangents at these points.

(k) If normal drawn to a parabola passes through a point \(\mathrm{P}(\mathrm{h}, \mathrm{k})\) then \(\mathrm{k}=\mathrm{mh}-2 \mathrm{am}-\mathrm{am}^{3}\) i.e. \(\mathrm{am}^{3}+\mathrm{m}(2 \mathrm{a}-\mathrm{h})+\mathrm{k}=0\).

Then gives \(\mathrm{m}_{1}+\mathrm{m}_{2}+\mathrm{m}_{3}=0 \quad ; \quad \mathrm{m}_{1} \mathrm{~m}_{2}+\mathrm{m}_{2} \mathrm{~m}_{3}+\mathrm{m}_{3} \mathrm{~m}_{1}=\frac{2 \mathrm{a}-\mathrm{h}}{\mathrm{a}} ; \mathrm{m}_{1} \mathrm{~m}_{2} \mathrm{~m}_{3}=-\frac{\mathrm{k}}{\mathrm{a}}\). where \(\mathrm{m}_{1}, \mathrm{~m}_{2} \& \mathrm{~m}_{3}\) are the slopes of the three concurrent normals. Note that the algebraic sum of the: slopes of the three concurrent normals is zero.

ordinates of the three conormal points on the parabola is zero.

Centroid of the \(\Delta\) formed by three co-normal points lies on the \(\mathrm{x}\)-axis.

(l) A circle circumscribing the triangle formed by three co-normal points passes through the vertex of the parabola and its equation is, \(2\left(x^{2}+y^{2}\right)-2(h+2 a) x-k y=0\)

Suggested problems from Loney: Exercise-25 (Q.5, 10, 13, 14, 18, 21, 22), Exercise-26 (Important) (Q.4, 6, 7, 17, 22, 26, 27, 28, 34), Exercise-27 (Q.4,), Exercise-28 (Q.2, 7, 11, 14, 23), Exercise-29 (Q.7, 8, 19, 21, 24, 27), Exercise-30 (2, 3, 18, 20, 21, 22, 25, 26, 30)

Note: Refer to the figure on Pg. 175 if necessary.

POSITION OFA POINT w.r.t. AN ELLIPSE :

The point \(\mathrm{P}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)\) lies outside, inside or on the ellipse according as \(; \frac{\mathrm{x}_{1}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}_{1}{ }^{2}}{\mathrm{~b}^{2}}-1><\mathrm{or}=0\).

AUXILIARY CIRCLE / ECCENTRICANGLE :

A circle described on major axis as diameter is called the auxiliary circle.

Let \(Q\) be a point on the auxiliary circle \(x^{2}+y^{2}=a^{2}\) such that QP produced is perpendicular to the \(\mathrm{x}\)-axis then P \& Q are called as the Corresponding Points on the ellipse \& the auxiliary circle respectively ' \(\theta\) ' is called the ECcentricAngLe of the point \(P\) on the ellipse \((0 \leq \theta<2 \pi)\)

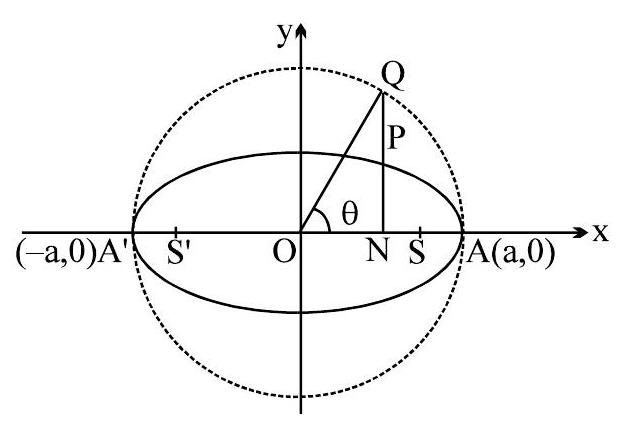
Note that \(\frac{\ell(\mathrm{PN})}{\ell(\mathrm{QN})}=\frac{\mathrm{b}}{\mathrm{a}}=\frac{\text { Semi minor axis }}{\text { Semi major axis }}\)

Hence "If from each point of a circle perpendiculars are drawn upon a fixed diameter then the locus of the points dividing these perpendiculars in a given ratio is an ellipse of which the given circle is the auxiliary circle".

4.PARAMETRIC REPRESENTATION :

The equations \(x=a \cos \theta \& y=b \sin \theta\) together represent the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\).

Where \(\theta\) is a parameter. Note that if \(\mathrm{P}(\theta) \equiv(a \cos \theta, \mathrm{b} \sin \theta)\) is on the ellipse then ; \(Q(\theta) \equiv(a \cos \theta, a \sin \theta)\) is on the auxiliary circle.

5.LINE AND AN ELLIPSE :

The line \(y=m x+c\) meets the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) in two points real, coincident or imaginary according as \(\mathrm{c}^{2}\) is \(<=\) or \(>\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}\)

Hence \(y=m x+c\) is tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) if \(c^{2}=a^{2} m^{2}+b^{2}\).

The equation to the chord of the ellipse joining two points with eccentric angles \(\alpha \& \beta\) is given by \(\frac{x}{a} \cos \frac{\alpha+\beta}{2}+\frac{y}{b} \sin \frac{\alpha+\beta}{2}=\cos \frac{\alpha-\beta}{2}\).

6. TANGENTS :

(i) \(\frac{\mathrm{xx}}{\mathrm{a}_{1}^{2}}+\frac{\mathrm{y}_{1}}{\mathrm{~b}^{2}}=1\) is tangent to the ellipse at \(\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)\).

Note : The figure formed by the tangents at the extremities of latus rectum is rhoubus of area \(\frac{2 a^{2}}{e}\)

(ii) \(y=m x \pm \sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}}\) is tangent to the ellipse for all values of \(\mathrm{m}\).

Note that there are two tangents to the ellipse having the same \(m\), i.e. there are two tangents parallel to any given direction.

(iii) \(\frac{x \cos \theta}{a}+\frac{y \sin \theta}{b}=1\) is tangent to the ellipse at the point \((a \cos \theta, b \sin \theta)\).

(iv) The eccentric angles of point of contact of two parallel tangents differ by \(\pi\). Conversely if the difference between the eccentric angles of two points is \(p\) then the tangents at these points are parallel.

(v) Point of intersection of the tangents at the point \(\alpha \& \beta\) is \(a \frac{\cos \frac{\alpha+\beta}{2}}{\cos \frac{\alpha-\beta}{2}}, b \frac{\sin \frac{\alpha+\beta}{2}}{\cos \frac{\alpha-\beta}{2}}\). 

AUXILIARY CIRCLE:

A circle drawn with centre \(\mathrm{C} \&\) T.A. as a diameter is called the AuXILIARY CIRCLE of the hyperbola. Equation of the auxiliary circle is \(x^{2}+y^{2}=a^{2}\).

Note from the figure that \(P \& Q\) are called the "Corresponding Points " on the hyperbola \& the auxiliary circle. ' \(\theta\) ' is called the eccentric angle of the point ' \(\mathrm{P}\) ' on the hyperbola. \((0 \leq \theta<2 \pi)\).

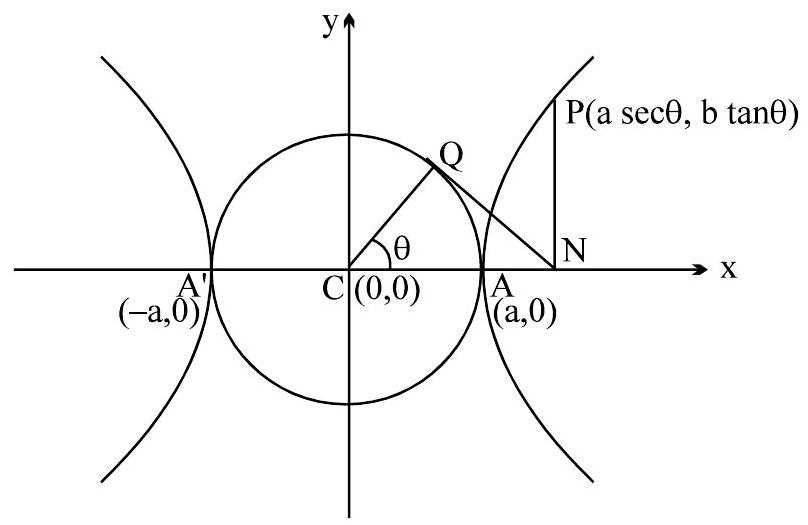
Note : The equations \(x=a \sec \theta \& y=b \tan \theta\) together represents the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) where \(\theta\) is a parameter. The parametric equations: \(\quad x=a \cos h \phi\), \(\mathrm{y}=\mathrm{b} \sin \mathrm{h} \phi\) also represents the same hyperbola.

General Note :

Since the fundamental equation to the hyperbola only differs from that to the ellipse in having \(-b^{2}\) instead of \(b^{2}\) it will be found that many propositions for the hyperbola are derived from those for the ellipse by simply changing the sign of \(\mathrm{b}^{2}\).

POSITION OFA POINT 'P' w.r.t. A HYPERBOLA:

The quantity \(\frac{\mathrm{x}_{1}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}_{1}^{2}}{\mathrm{~b}^{2}}=1\) is positive, zero or negative according as the point \(\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)\) lies within, upon or without the curve.

LINE AND A HYPERBOLA :

The straight line \(y=m x+c\) is a secant, a tangent or passes outside the hyperbola \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) according

as: \(c^{2}>=<a^{2} m^{2}-b^{2}\).

8. TANGENTS AND NORMALS :

TANGENTS :

(a) Equation of the tangent to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) at the point \(\left(x_{1}, y_{1}\right)\) is \(\frac{x_{1}}{a^{2}}-\frac{y y_{1}}{b^{2}}=1\).

Note: In general two tangents can be drawn from an external point \(\left(\mathrm{x}_{1} \mathrm{y}_{1}\right)\) to the hyperbola and they are \(\mathrm{y}-\mathrm{y}_{1}=\mathrm{m}_{1}\left(\mathrm{x}-\mathrm{x}_{1}\right) \& \mathrm{y}-\mathrm{y}_{1}=\mathrm{m}_{2}\left(\mathrm{x}-\mathrm{x}_{2}\right)\), where \(\mathrm{m}_{1} \& \mathrm{~m}_{2}\) are roots of the equation \(\left(\mathrm{x}_{1}^{2}-\mathrm{a}^{2}\right) \mathrm{m}^{2}-2 \mathrm{x}_{1} \mathrm{y}_{1} \mathrm{~m}+\mathrm{y}_{1}^{2}+\mathrm{b}^{2}=0\). If \(\mathrm{D}<0\), then no tangent can be drawn from \(\left(\mathrm{x}_{1} \mathrm{y}_{1}\right)\) to the hyperbola.

(b) Equation of the tangent to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) at the point \((a \sec \theta, b \tan \theta)\) is \(\frac{x \sec \theta}{a}-\frac{y \tan \theta}{b}=1\). Note : Point of intersection of the tangents at \(\theta_{1} \& \theta_{2}\) is \(x=a \frac{\cos \frac{\theta_{1}-\theta_{2}}{2}}{\cos \frac{\theta_{1}+\theta_{2}}{2}}, y=b \frac{\sin \frac{\theta_{1}+\theta_{2}}{2}}{\cos \frac{\theta_{1}+\theta_{2}}{2}}\)

(c) \(\quad y=m x \pm \sqrt{a^{2} m^{2}-b^{2}}\) can be taken as the tangent to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\).

Note that there are two parallel tangents having the same slope \(\mathbf{m}\).

(d) Equation of a chord joining \(\alpha \& \beta\) is

\(\frac{\mathrm{x}}{\mathrm{a}} \cos \frac{\alpha-\beta}{2}-\frac{\mathrm{y}}{\mathrm{b}} \sin \frac{\alpha+\beta}{2}=\cos \frac{\alpha+\beta}{2}\)

In order that \(y=m x+c\) be an asymptote, both roots of equation (1) must approach infinity, the conditions for which are :

coeff of \(x^{2}=0 \&\) coeff of \(x=0\).

\(\Rightarrow \quad b^{2}-a^{2} m^{2}=0\) or \(m=\pm \frac{b}{a} \&\) \(\mathrm{a}^{2} \mathrm{mc}=0 \Rightarrow \mathrm{c}=0\)

\(\therefore\) equations of asymptote are \(\frac{\mathrm{x}}{\mathrm{a}}+\frac{\mathrm{y}}{\mathrm{b}}=0\) and \(\quad \frac{x}{a}-\frac{y}{b}=0\).

combined equation to the asymptotes \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=0\).

PARTICULAR CASE :

When \(b=a\) the asymptotes of the rectangular hyperbola.

Note :

\(x^{2}-y^{2}=a^{2} \text { are, } y=\pm x \text { which are at right angles. }\)

(i) Equilateral hyperbola \(\Leftrightarrow\) rectangular hyperbola.

(ii) If a hyperbola is equilateral then the conjugate hyperbola is also equilateral.

(iii) A hyperbola and its conjugate have the same asymptote.

(iv) The equation of the pair of asymptotes differ the hyperbola & the conjugate hyperbola by the same constant only.

(v) The asymptotes pass through the centre of the hyperbola & the bisectors of the angles between the asymptotes are the axes of the hyperbola.

(vi) The asymptotes of a hyperbola are the diagonals of the rectangle formed by the lines drawn through the extremities of each axis parallel to the other axis.

(vii) Asymptotes are the tangent to the hyperbola from the centre.

(viii) A simple method to find the coordinates of the centre of the hyperbola expressed as a general equation of degree 2 should be remembered as:

Let \(\mathrm{f}(\mathrm{x}, \mathrm{y})=0\) represents a hyperbola.

Find \(\frac{\partial \mathrm{f}}{\partial \mathrm{x}} \& \frac{\partial \mathrm{f}}{\partial \mathrm{y}}\). Then the point of intersection of \(\frac{\partial \mathrm{f}}{\partial \mathrm{x}}=0 \& \frac{\partial \mathrm{f}}{\partial \mathrm{y}}=0\) gives the centre of the hyperbola.

HIGHLIGHTS ONASYMPTOTES:

H-1 If from any point on the asymptote a straight line be drawn perpendicular to the transverse axis, the product of the segments of this line, intercepted between the point & the curve is always equal to the square of the semi conjugate axis.

H-2 Perpendicular from the foci on either asymptote meet it in the same points as the corresponding directrix \(\&\) the common points of intersection lie on the auxiliary circle.

H-3 The tangent at any point \(P\) on a hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) with centre \(C\), meets the asymptotes in \(Q\) and \(R\) and cuts off a \(\triangle \mathrm{CQR}\) of constant area equal to ab from the asymptotes & the portion of the tangent intercepted between the asymptote is bisected at the point of contact. This implies that locus of the centre of the circle circumscribing the \(\triangle \mathrm{CQR}\) in case of a rectangular hyperbola is the hyperbola itself \& for a standard hyperbola the locus would be the curve, \(4\left(a^{2} x^{2}-b^{2} y^{2}\right)=\left(a^{2}+b^{2}\right)^{2}\).

H-4 If the angle between the asymptote of a hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) is \(2 \theta\) then \(e=\sec \theta\). Q.12 The tangents & normal at a point on \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) cut the \(y-\) axis at A \& B. Prove that the circle on \(A B\) as diameter passes through the foci of the hyperbola. Q.13 The perpendicular from the centre upon the normal on any point of the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) meets at

R. Find the locus of \(R\).